ما هو الكسر العشري ، وما علاقته بالكسر العادي ؟

تمهيد :

 نقول أن الكسر العشري حالة من حالات الكسر العادي مقامه العشرة أو مضاعفاتها (10 ، 100 ، ... )

 وتُستعمل في الكسر العشري الفاصلة العشرية ( , ) بدل خط الكسر ، وسميت كذلك لأنها تفصل بين الأعداد الصحيحة والأجزاء العشرية .

2) عرفت سابقاً أن العدد 76.583 مكون من

7 عشرات صحيحة أي   70

لاحظ هنا أن الوحدة المميزة مقسومة في الكسر العشري إلى 10 أقسام متساوية أو 100 من الأقسام المتساوية أو  1000 من الأقسام المتساوية ... الخ .

 ويبين الكسر العشري عدد الأقسام الموجودة في كل فئة .

تحويل الكسر العادي إلى كسرٍ عشري

الأهداف :ـ  أن يتقن الدارس عملية تحويل الكسور العادية إلى كسور عشرية .

 الخبرات السابقة :
ـ الكسور والأعداد الكسرية ، الكسور العشرية ، عمليات القسمة الطويلة ، مفهوم الضرب في الواحد الصحيح .

الإجراءات والأنشطة :

أ. تعلمت سابقاً أن الكسور العادية التي يكون مقامها 10 ، 100 ، 1000 … الخ ، يمكن تحويلها بسهولة إلى كسر عشري ، ذلك لأن هذه الكسور هي أعشار أو أجزاء من مئة أو أجزاء من ألف … ، وتكون أجزاؤها العادية كأجزاء الكسور العشرية .

ب. الكسور العادية التي مقاماتها ليست العشرة أو مضاعفاتها (قواها) .

 1) يُمكن تحويل الكسور العادية إلى كسور عشرية وذلك بضرب كل من البسط والمقام في العدد الذي يجعل مقام الكسر العادي العشرة أو مضاعفاتها  10 ، 100 ، 1000 ... وهكذا .

إلى كسر عشري .

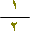مثال (1) : حوِّل الكسر

الحل :

إلى كسر عشري .

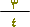مثال (2) : حوِّل الكسر

الحل :

الكسور المنتهية والكسور الدورية

1) الكسور المنتهية والكسور الدورية  

الهدف : أن يتعرف الدارس إلى مفهوم الكسر المنتهي والكسر الدوري (وأن يميز بينهما) . 

الخبرات السابقة : تحويل الكسور العادية والأعداد الكسرية إلى كسور عشرية ، عملية القسمة الطويلة .

 الإجراءات والأنشطة :

 الكسور المنتهية

تمهيد : ادرس الأمثلة التالية ولاحظ أن عمليات القسمة التي نجريها ، لتحويل هذه الكسور العادية إلى كسور عشرية ، قد انتهت (باقي القسمة يساوي صفر) .

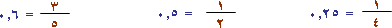إلى كسور عشرية بإجراء عمليات القسمة :

،

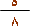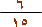أ) حوِّل الكسر

الحل :

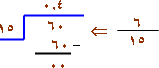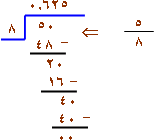لاحظ هنا أن عمليات القسمة لتحويل الكسور في الأمثلة السابقة انتهت (باقي القسمة يساوي صفراً) .

نُسمي الكسور العشرية الناتجة كسوراً منتهية

عند تحويل الكسور التالية إلى كسور عشرية بإجراء عمليات القسمة نجد أن باقي القسمة في كل حالة يساوي صفراً ، ونسمي الكسور العشرية الناتجة كسوراً منتهية .

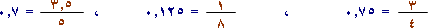الكسور الدورية

الرقم الدوري والرقم غير الدوري في الكسور العشرية الدورية

 الهدف : أن يتعرف الدارس إلى الأرقام الدورية وكيفية كتابتها وقراءتها . 

الخبرات السابقة : الكسور المنتهية والكسور الدورية . 

الإجراءات والأنشطة :

حوِّل الكسور التالية إلى كسور عشرية وادرس جيداً الرقم أو الأرقام الناتجة عن إجراء عمليات القسمة في كل واحد منها .

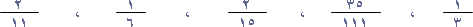
نُسمي كل كسر من هذه الكسور العشرية "كسراً عشرياً دورياً" .

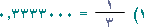
إلى كسر عشري عن طريق قسمة البسط (1) على المقام (3) قسمة فعلية . وإذا

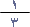يتم تحويل الكسر

قمت بإجراء عملية القسمة هذه تُلاحظ أن العدد نفسه يتكرر في ناتج القسمة باستمرار ، ولا يمكن أن نصل إلى وضع يكون الباقي فيه صفراً .      

أي يُكتفى

إن الرقم الدائر في هذا الكسر العشري 0.33333 هو (3) ويُكتب الكسر العشري على صورة

بكتابة الرقم الدوري بعد الفاصلة العشرية ويوضع فوقه خط ويُقرأ : صفر فاصلة ثلاثة بالعشرة والرقم 3 دوري .

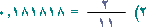
أي يُكتفى

إن الأرقام الدورية في هذا الكسر العشري هي 18 على الترتيب ويكتب الكسر على صورة

 بكتابة رقمي الدورة بعد الفاصلة العشرية ويُقرأ : 18 بالمئة ، والعدد 18 دوري .

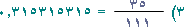
أي يُكتفى

إن الأرقام الدورية في هذا الكسر هي 315 على الترتيب ويُكتب الكسر على صورة

بكتابة أرقام الدورة بعد الفاصلة العشرية ويُقرأ 315 بالألف والعدد 315 دوري .

تحويل الكسر العشري إلى كسرٍ عادي

الأهداف : أن يتقن الدارس عمليات تحويل الكسور العشرية إلى كسور عادية أو أعدادٍ كسرية .

 الخبرات السابقة : الكسور والأعداد الكسرية ، الكسور العشرية ، عمليات القسمة الطويلة .

 الإجراءات والأنشطة :

من المتر أو 0.25 من المتر .

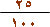أ) تعلمت سابقاً أن 25 سم =

من المتر أو 0.6 من المتر .

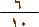وأن 6 دسم =

من الكيلوغرام أو 0.75 من الكيلوغرام .

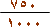وكذلك 750 غم =

    

لاحظ هنا أنَّ

		،		،

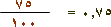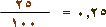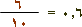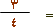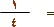يُمكن تحويل الكسر العشري إلى كسر عادي ، بإعادة الكسر العشري إلى الكسر العادي المكافئ الذي يكون مقامه عادة العشرة أو مضاعفاتها 10 ، 100 ، 1000 ...

تدريب : حوِّل الكسور العشرية التالية إلى كسور عادية بأبسط صورة :

           7.0 =        ،        0.35 =     ،       0.025 =

ضرب الكسور العشرية

الإجراءات والأنشطة :

تمهيد : أ. تحويل الكسور العشرية إلى كسور عادية ثم إجراء عمليات الضرب .

1) أوجد ناتج : 2.8 × 3.15

 الحل :

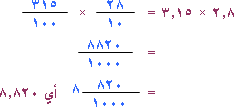لاحظ أن الناتج احتوى على عدد من المنازل العشرية مساوياً لمجموع عدد المنازل العشرية في المضروب والمضروب فيه .

2) أوجد ناتج 6 × 0.72

 الحل :

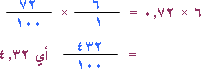لاحظ أن الناتج احتوى على عدد من المنازل العشرية مساوياً لمجموع عدد المنازل العشرية في المضروب والمضروب فيه .

3) أوجد ناتج 3.05 × 0.05

 الحل :

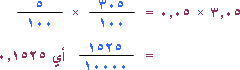لاحظ أن الناتج احتوى على عدد من المنازل العشرية مساوياً لمجموع عدد المنازل العشرية في المضروب والمضروب فيه .

قسمة الكسور العشرية على 10 ، 100 ، 1000 ... الخ .

  تمهيد :

يُكتب على الصورة 45.3

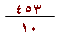1) أنت تعرف أن الكسر

          

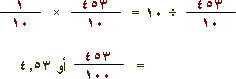وتعرف أن

وبالتالي 45.3 ÷ 10 = 4.53 لاحظ هنا أننا حركنا الفاصلة عن موضعها عند القسمة إلى اليسار منزلة عشرية واحدة .

وكذلك

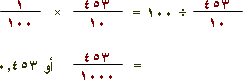وهكذا

65.2 ÷ 10 = 6.52

65.2 ÷ 100 = 0.652

65.2 ÷ 1000 = ؟؟؟          0.0652

65.2 ÷ 10000 = ؟؟         0.00652

عند قسمة كسر عشري على العشرة (10) أو على مضاعفاتها (قواها) نحرك الفاصلة إلى اليسار عدداً يساوي عدد الأصفار في مضاعفات (قواها) العشرة .

وإذا انتهت المنازل دون استيفاء عدد المنازل المطلوب ، نكملها بوضع صفر أو أكثر على يسار العدد حتى يتم العدد المعين للمنازل .