الأحد، 10 نوفمبر 2013

بعض المتطلبات المسبقة :
حتى تفهم المعادلة  التربيعية وطرق حلها عليك أن تكون دارساً وفاهماً للموضوعات التالية :-
1) الحدود والمقادير الجبرية .
2) تمثيل الاقتران التربيعيي بيانياً .
3) تحليل العبارة التربيعية .
فيما يلي سنعالج الحدود والمقادير الجبرية بشئ من التفصيل .

تمهيد :
 نستخدم في علم الجبر الرموز والأعداد في التعبير عن الكميات ، فمثلاً نجد 2س ، ص + 5 ، س+ 6 ،
   د2 ﻫ 2 + 2 د + 5 ﻫ - 7 ....... إلخ وكلها تعبر عن مقادير جبرية. أطلق علماء الرياضيات على هذه  الكميات تسميات خاصة اعتماداً على ما نجد فيها من متغيرات ومن قوى لهذه المتغيرات ونتعرف فيما يلي على بعض هذه التسميات والمصطلحات.
 
1. الحد الجبري monomial or term :
 وهو مقدار جبري يتكون من متغير واحد، أو من عدة متغيرات مضروبة في بعضها، أما معامله فيكون عدداً حقيقياً وأما قوته فتكون عدداً صحيحاً موجباً، وهذه أمثلة :
1) 2س3 : الرمز المستخدم  س ، المعامل (2) ، القوة (3) .
2)  ب  : الرمز المستخدم  ب ، المعامل  1 ، والقوة (1).
 , القوة (5) .
 ص5 : والرمز ص، المعامل
3)
4) 5س3 ص2 : المعامل 5، قوة س (3) وقوة ص (2) وكلها مضروبة في بعضها.
5)  3ع2 ل6 ك : المعامل  3، والمتغيرات ثلاثة بقوى مختلفة ولكنها كلها مضروبة في بعضها وهو الشرط الأساس في اعتبارها حداً جبرياً واحداً.

2. كثير الحدود polynomial :
 هو مقدار جبري يتكون من حدين أو أكثر يفصل بينهما إشارة ( + ) أو (  ) أما معاملاتها فتكون أعداد حقيقية وقواها صحيحة موجبة.
أمثلة :
1) أ  3  كثير حدود يتكون من حدين . لاحظ أن العدد ( الذي نسميه عادة الحد المطلق ) يعتبر حداً  من حدود المقدار مثله مثل أي متغير .
2) ص2  3ص + 2  كثير حدود يتكون من ثلاثة حدود .
3)  س3 +  2س2  3س + 1  كثير حدود .
4) س2  2س ص + ص2 كثير حدود يتكون من ثلاثة حود جبرية ولكن عدد المتغيؤات اثنان هما س، ص.
مقدار جبري يتكون من خمسة حدود أما عدد المتغيرات فهو ستة.
5)


بعض المصطلحات الخاصة بكثيرات الحدود:
1. ثنائي الحدودbinomial  : أي مقدار جبري يتكون من حدين ، أو أي كثير حدود يتكون من حدين فقط،  مثلاً 5س + 2ص  أو ل3  8 أو  3 س ص  4 ل ع.

2. ثلاثي الحدود trinomial  : هو كثير حدود يتكون من ثلاثة حدود فقط مثل :
5 ﻫ + 7س  2ل  ، 7 ص 2 3 ل2 +1 ، 5 ك م  4 أ2 جـ3 + ب5.

 3. ثلاثي الحدود التربيعي أو العبارة التربيعية : هذا مصطلح يخص كثير حدود يتكون من متغير واحدوثلاثة حدود وصيغته العامة هي أ س2 + ب س + جـ  حيث أ ، ب ، جـ ، أعداد حقيقية وحيث أ ≠صفر لأنه في هذه الحالة لايعود المقدار تربيعياً .

ملاحظة هامة: قد يتكون ثلاثي الحدود التربيعي من متغيرين وفي هذه الحالة يأخذ الصيغة العامة التالية أ س2 + ب س ص + جـ ص2 حيث أ ، ب ، جـ أعداد حقيقية وليس أي واحد منها = صفراً.

 العبارة التربيعية: تأمل الأمثلة الثلاثة التالية، إن كل واحد منها هو ثلاثي حدود بمتغير واحد.
1) 5 ل2  2 ل +3 .
2) 3س2 + 8س + 5.
3)  2ص2  4ص + 15 .

وعادة ما نعطيها الشكل العام أ س2 + ب س + جـ .
يمكن أن تكون ب = صفر ( تذكر أننا نرمز لمعامل المتغير  س بالرمز ب )  وفي هذه الحالة يصبح ثلاثي الحدود على شكل " أس2 + جـ "  لأن الحد الأوسط  ب س = 0
ويمكن أن نطلق على المقدار في هذه الحالة اسم ثنائي حدود تربيعي أو ثلاثي حدود تربيعي .
أماإذا كانت جـ = صفر (تذكر أننا نرمز للحد المطلق بالرمز جـ) فإن ثلاثي الحدود يصبح
 أ س2 + ب س + صفر. 
 وهو أيضاً ثنائي حدود تربيعي أ س2 + ب س  أو ثلاثي حدود تربيعي أس2 + ب س + صفر  .

أما إذا كانت ب = ﺠ = الصفر  فإن المقدار أ س2 + ب س + جـ = أ س2 يصبح مكوناُ من حد واحدmonomial  أي يصبح حداً جبرياً وليس ثلاثي حدود .

الخلاصة:
العبارة التربيعية أو ما نسميه أيضاً ثلاثي الحدود التربيعي :
 هو أي مقدار من الشكل العام  أس2 + ب س + جـ  حيث لايمكن أن تكون أ = .
 ولايمكن أن تكون  ب = جـ = . 

- مفهوم المعادلة التربيعية :

 هي اقتران تربيعي حينما يكون ق (س) = صفر.

مثال:
ق ( س ) = أ س2 + ب س + جـ  هو اقتران تربيعي  فإذا كان ق (س) =0 فإن الاقتران يؤول إلى 
0 = أ س2 + ب س + ﺠ  معادلة تربيعية .
لاحظ أن 7 = أ س2 + ب س + د  هو معادلة تربيعية
لأن   أ س2 + ب س + د  7 = 0 حيث يمكن أن نقول في هذه الحالة أن  جـ = د  7.
 
حل المعادلة التربيعية:

 لقد تعلمنا سابقاً، في المعادلات التي يكون المجهول فيها من الدرجة الأولى أن حل المعادلة تعني إيجاد قيمة المجهول وفي حالة المعادلة التربيعية لا يختلف الأمر ، فحلها يعني إيجاد قيمتي (سنجد أن للمجهول  قيمتين لأن المعادلة تربيعية) المجهول الوارد فيها .



حل المعادلة التربيعية:

 لقد تعلمنا سابقاً، في المعادلات التي يكون المجهول فيها من الدرجة الأولى أن حل المعادلة تعني إيجاد قيمة المجهول وفي حالة المعادلة التربيعية لا يختلف الأمر ، فحلها يعني إيجاد قيمتي (سنجد أن للمجهول قيمتين لأن المعادلة تربيعية) المجهول الوارد فيها .

طرق حل المعادلة التربيعية:
 يمكن حل المعادلة التربيعية بعدة طرق، منها إعادتها إلى أصلها وهو الاقتران التربيعي، ومنها طريقة التحليل إلى العوامل ، وطريقة القانون العام كل هذه الطرق تختلف عن بعضها قليلاً وفي أمور تفصيلية أما أساسها فهو واحد.
سنطبق هذه الطرق المختلفة على مثال واحد لنقارن بينها ولنتمكن من ربطها ببعضها .

حل المعادلة : س2  6س + 5 = 0
مثال :
1) الطريقة الأولى : عمل جدول بقيم س ، ق ( س ) المقابلة لها .
الحل :  المعادلة المطلوب حلها هي  س2  6س + 5 = 0
اختر قيماً لـِ س في الفترة ( 5، +5 )، ثم أوجد قيم  ق (س) المقابلة. يكون حل المعادلة هو قيم س التي يكون عندها ق (س)  = الصفر .
جدول بقيم س ، ق(س) المقابلة لها
5
4
3
2
1
صفر
1
2
 3
4
5
س
صفر
3
4
3
صفر
5
12
21
32
45
60
ق(س)
وكماهو واضح من الجدول يكون حل المعادلة هو :  س = 1   و   س = 5 .


2) الطريقة الثانية :
الحل برسم منحنى الاقتران ( القطع المكافئ ) ق (س) = س2  6 س + 5  المقابل للمعادلة.
الحل:
في هذه الطريقة نضع جدولاً بقيم نختارها للمتغير في الاقتران ونجد قيم ق (س) المقابلة لها ، كما هو الحال مع ما قمنا به بالطريقة الأولى .
6
5
4
3
2
1
صفر
س
5
صفر
3
4
3
صفر
5
ق (س)
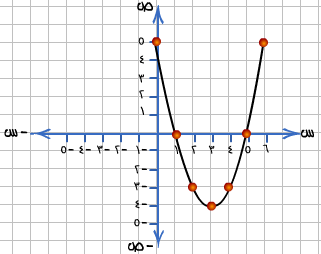نرسم منحنى الاقتران ونجد نقاط تقاطعه مع محور السينات (ص = صفر) فتكون قيم س عند هذه النقط هي حل المعادلة .

ارسم المنحنى بدقة ( أو باستخدام الحاسوب ) تجد أنه يتقاطع مع محور السينات عند النقطتين  س = 1 ،   س = 5 .
أي أن حل المعادلة هو   س = 1  و  س = 5 .
- ملاحظات على الطريقتين السابقتين :
1. إذا كانت قيم المجهول في المعادلة التربيعية قيماً كسرية أو أعداداً غير نسبية فلن تظهر في الجدول ولكنها ستظهر بشكل تقريبي على منحنى القطع المكافئ، لذلك عند الرسم يجب مراعاة الدقة كما يفضل استخدام الحاسوب في رسم المنحنى .
أمثلة :
 

3)  س2 – 8.2 س +16 = صفر    س ¬  3.2 ، 5 .


2. إذا كانت قيم المجهول كبيرة مثلاً في معادلات مثل :
س2  23 س  570 = صفر         حيث س = 38  و  15 فيجب مراعاة الأمر عند الرسم واستخدام مقياس مناسب حيث 1سم على ورقة المربعات يمكن أن يمثل  5  أو عشر وحدات .....إلخ.
إن عمل جدول بقيم س ، ق ( س ) في مثل هذه الحالات يتطلب بعض الوقت .
يفضل استخدام الطريقتين السابقتين حينما تكون قيم المجاهيل صغيرة مثلاً  10 ³   س  ³ +10 .

3. نعود ونؤكد عند استخدام هاتين الطريقتين ( وهما في الواقع طريقة واحدة حيث أن ارتباط الواحدة بالأخرى يكون عضوياً ) على ضرورة الرسم بمنتهى الدقة والأفضل أن يكون رسم المنحنى باستخدام الحاسوب إذا كان الدارس قادراً على ذلك .





3) الطريقة الثالثة:  
طريقة التحليل إلى العوامل الأولية هذه طريقة سهلة تعتمد على ما تعلمت سابقاً تحت عنوان " تحليل العبارة التربيعية ".
 حل  المعادلة س2 6 س +5 = صفر  بالتحليل إلى العوامل .
 الحل:
الطرف الأيمن في المعادلة س2 6 س +5 = صفر  هو مقدار ثلاثي حدود تربيعي ( أي عبارة تربيعية ) يمكن تحليله بسهولة كما تعلمنا حيث نبحث عن عددين حاصل ضربهما + 5 ومجموعهما  6 ، نجد أن هذين العددين هما   1 ،  5 ،  إذن :
س2  6 س +5 = صفر  ( س  5 )( س  1 ) = صفر .
حصلنا على مقدارين هما ( س  5 ) و ( س  1 ) حاصل ضربهما = صفر وهذا لا يمكن إلا إذا كان أحد المقدارين أو كلاهما = الصفر.
إذا فرضنا أن   س  5 = صفر  تكون  س = 5
وإذا فرضنا أن  س  1 = صفر  تكون  س = 1
هذه الطريقة تصلح ما دام  الدارس قادراً على تحليل العبارة التربيعية بسهولة ودون عناء  مثلاً:
س2  7 س  18 = صفر .
حيث تحليل  س2  7 س  18  هو  (س  9) (س + 2)
إذن (س  9) (س + 2) = صفر  .
إذن   س =  9
ومنه  س  9 =  صفر
إذن  س = 2
ومنه س + 2 = صفر 
أي أن  س = 9  ،  2 .

أما إذا كان الأمر يتعلق بمعادلات من النمط :
أ)  14 س2 +  س  30 = صفر    قابلة للتحليل في قوسين .
ب)  س2 + 4 س  117 = صفر    قابلة للتحليل في قوسين.
ج)  س2  7 س  + 11 = صفر     غير قابلة للتحليل .
في مثل هذه الحالات علينا أن نبحث عن طريقة أخرى غير طريقة التحليل إلى العوامل ، وغير الطريقتين الأولى والثانية أيضاً.

4) الطريقة الرابعة :  حل المعادلة التربيعية باستخدام القانون .

تمهيد:
قبل أن نعطيك القانون جاهزاً يحق لك أن تتساءل كيف توصلنا اليه ، وكيف يمكنك أن تتوصل إليه بنفسك؟
هذا ما سنحاول الإجابة عليه تالياً من خلال هذه المناقشة مع الدارس .
 ـ ماهي الصيغة العامة للمعادلة التربيعية ؟   الصيغة العامة هي أ س2 + ب س + ﺠ = صفر.
 ـ ما هو معامل  س2  في المعادلة ؟  الجواب ......
ـ ما ناتج قسمة المعادلة على أ ؟
الجواب :
لطرفي المعادلة .....(1) ماذا ينتج عن ذلك ؟
أضف 
ـ كيف تجعل الطرف الأيمن مربعاً كاملاً ؟
مميز المعادلة التربيعية:

مميز المعادلة التربيعية :
 
الأهداف :
 عزيزي الدارس يتوقع منك بعد دراسة هذا الدرس أن تكون قادراً على التعرف على مميز المعادلة التربيعية واستخدام المميز في معرفة نوع المعادلة إن كانت تحلل أو لا.

تمهيد : هل يمكن إيجاد جذور لجميع المعادلات التربيعية ؟
ـ ما جذور المعادلة س2 + س + 12 = صفر  ؟
ـ ما جذور المعادلة س2 + 1 = صفر  ؟
لو بحثت في إيجاد حل للمعادلتين السابقتين أي إيجاد جذور كل منهما فلن تجد لهما حلاً .
أي ليست كل المعادلات التربيعية يمكن حلها .
 
والسؤال الآن : كيف يمكن أن نميز بين المعادلات التربيعية التي يمكن حلها والتي لا حل لها ؟
الجواب : هو استخدام المميز ( ب2  4 أ جـ) حيث ب هو معامل س ، أ هو معامل س2 ، جـ الحد المطلق .
إن مميز المعادلة التربيعية ( ب2  4أ جـ ) هو الذي يحدد إذا كان للمعادلة جذور ( لها حل ) أو لا جذور لها ( ليس لها حل ) حيث إذا كان المميز أكبر من الصفر ( موجب ) أو يساوي صفراً فإن المعادلة لها حل .أما إذا كان أقل من الصفر فإن المعادلة ليس لها حل .
وبالرموز :
ب2  4 أ جـ ≤  صفر لها حل .
ب2  4 أ جـ < صفر ليس لها حل .

شرح المعادلة التربعية:

مرسلة بواسطة في

ليست هناك تعليقات:

إرسال تعليق

الاشتراك في: تعليقات الرسالة (Atom)